Greenhouse Effect
Emuskald is an avid horticulturist and owns the world's longest greenhouse — it is effectively infinite in length.
Over the years Emuskald has cultivated n plants in his greenhouse, of m different plant species numbered from 1 to m. His greenhouse is very narrow and can be viewed as an infinite line, with each plant occupying a single point on that line.
Emuskald has discovered that each species thrives at a different temperature, so he wants to arrange m - 1 borders that would divide the greenhouse into m sections numbered from 1 to m from left to right with each section housing a single species. He is free to place the borders, but in the end all of the i-th species plants must reside in i-th section from the left.
Of course, it is not always possible to place the borders in such way, so Emuskald needs to replant some of his plants. He can remove each plant from its position and place it anywhere in the greenhouse (at any real coordinate) with no plant already in it. Since replanting is a lot of stress for the plants, help Emuskald find the minimum number of plants he has to replant to be able to place the borders.
Input
The first line of input contains two space-separated integers n and m (1 ≤ n, m ≤ 5000, n ≥ m), the number of plants and the number of different species. Each of the following n lines contain two space-separated numbers: one integer number si (1 ≤ si ≤ m), and one real number xi (0 ≤ xi ≤ 109), the species and position of the i-th plant. Each xi will contain no more than 6 digits after the decimal point.
It is guaranteed that all xi are different; there is at least one plant of each species; the plants are given in order "from left to the right", that is in the ascending order of their xi coordinates (xi < xi + 1, 1 ≤ i < n).
Output
Output a single integer — the minimum number of plants to be replanted.
Sample test(s)
input
3 2 2 1 1 2.0 1 3.100
output
1
input
3 3 1 5.0 2 5.5 3 6.0
output
0
input
6 3 1 14.284235 2 17.921382 1 20.328172 3 20.842331 1 25.790145 1 27.204125
output
2
Note
In the first test case, Emuskald can replant the first plant to the right of the last plant, so the answer is 1.
In the second test case, the species are already in the correct order, so no replanting is needed.
------------------------------------editorial----------------------------------
Problem
There are n points on the line, each of type from 1 to m. We can freely divide the line into m - 1 intervals and replace some points so each point with type i is inside the i-th interval numbered 1 to m from left to right. We must find the minimum number of points to replace.
Solution
First, observe that the coordinates don’t matter: only the order of the points is important. Let there be some number of points we can replace to achieve the good arrangement. Then all the other points remain in their positions, so their values must be in increasing order from left to right. Then we must find the maximum number of points that can remain in their positions, which is the longest non-decreasing subsequence of types in the input. If it is of length l, the answer is n - l.
In this problem it was enough to implement a quadratic solution. We count dp[i][j] — the length of the longest non-decreasing subsequence on prefix [1;i], with element of type j being the last in subsequence. The transition is as follows:

For easy implementation, we can maintain only array dp[j], and skip the second case.
Time: O(n2) / 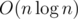 .
.
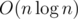 .
.
Memory: O(n2) / O(n).
Implementation: C++
-------------------------------------------------code---------------------------------------------------------------
#include<bits/stdc++.h>
using namespace std;
vector<int> v;
int dp[100000];
int main()
{
int n,m;
cin>>n>>m;
for(int i=0;i<n;i++)
{
int a;
cin>>a;
float f;
cin>>f;
v.push_back(a);
}
dp[0]=1;
int ans=0;
for(int i=0;i<n;i++)
{
int num=v[i];
int maxi=1;
for(int k=i-1;k>=0;k--)
{
if(v[k]<=num)
{
maxi=max(maxi,dp[k]+1);
}
}
dp[i]=maxi;
ans=max(ans,maxi);
}
cout<<n-ans<<endl;
}
No comments:
Post a Comment