C. Number of Ways ( number of ways in which we can divide an array in 3 parts with equal sum)

C. Number of Ways

You've got array a[1], a[2], ..., a[n], consisting of n integers. Count the number of ways to split all the elements of the array into three contiguous parts so that the sum of elements in each part is the same.

More formally, you need to find the number of such pairs of indices i, j (2 ≤ i ≤ j ≤ n - 1), that .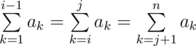

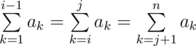Input

The first line contains integer n (1 ≤ n ≤ 5·105), showing how many numbers are in the array. The second line contains n integers a[1],a[2], ..., a[n] (|a[i]| ≤  109) — the elements of array a.

Output

Print a single integer — the number of ways to split the array into three parts with the same sum.

Examples

input

5
1 2 3 0 3

output

2

input

4
0 1 -1 0

output

1

input

2
4 1

output

0

-----------------------------------------------EDITORIAL----------------------------------------------------------

First of all, notice that if sum of all elements is equal S then sum of each of three parts is equal .
Therefore, if S is not divided by 3 — then answer is 0.
Otherwise, let’s iterate the end of first part i (1 ≤ i ≤ n - 2) and if sum of 1..i elements is equal  then it means that we have to add to the answer the amount of such j (i + 1 < j) that the sum of elements from j-th to n-tn also equals .

Let’s create an array cnt[], where cnt[i] equals 1, if the sum of elements from i-th to n-th equals  and 0 — otherwise. Now, to calculate the answer we have to find the sum cnt[j] + cnt[j+1] + ... + cnt[n] faster then O(n). There are a lot of required ways to do this, but the easiest one is to create a new additional array sums[] where in j-th element will be cnt[j] + cnt[j+1] + ... + cnt[n]. It is easy to calculate in such way: sums[n] = cnt[n], sums[i] = sums[i+1] + cnt[i] (i < n).

Thus, we receive very simple solution: for each prefix of initial array 1..i with the sum that equals  we need to add to the answersums[i+2].

-----------------------------------------------------------------------CODE----------------------------------------------------------

#include<bits/stdc++.h>

using namespace std;

typedef long long int lli;

lli arr[1000000];

int fw[1000000];

lli sum=0;

int main()

{

int n;cin>>n;

for(int i=1;i<=n;i++)

 {

   cin>>arr[i];

    sum+=arr[i];

 }

  //cout<<"sumis "<<sum<<endl;

 if(sum%3!=0)

 {

   cout<<0<<endl;

   return 0;

 }

 lli temp=0;

 

 for(int i=1;i<=n;i++)

 {

  if(temp+arr[i]==sum/3)

  {

  fw[i]=fw[i-1]+1;

 }

 else fw[i]=fw[i-1];

 temp+=arr[i];

 }

 //for(int i=1;i<=n;i++) cout<<fw[i]<<" ";

 lli ans=0;

 temp=0;

 for(int i=1;i<=n-1;i++)

  {

    temp+=arr[i];

    // cout<<temp<<endl;

    if(temp==2*(sum/3))

    {

     // cout<<" check "<<i<<endl;

       ans+=fw[i-1];

 }

  

  }

 cout<<ans<<endl;

}